[Incremental Learning] Hybrid-based 방법론을 훑어보자(RPS-Net ,FRCL)

0. Overview

• 지금까지 전개된 CL 방법론 들은 크기 (1) Regularization based 방법과 (2) Rehearsal 방법으로 나뉜다. 하지만 hybrid 방법은 이 두가지는 각각 단점이 있다고 생각하고, 이들을 합쳐서 사용하는 방법이다. 
  • (1) Regularization based : 대부분의 방법이 task boundaries를 요구하고, representation drift에 민감하다. (New task가 들어오면, 기존에 최적화된 파라미터는 obsolete(무용지물)이 된다.) 
  • (2) Rehearsal based : 어떤 data를 저장할지는 heruistics하게 결정된다. 

 

1. RPS-Net

Random Path Selection for Incremental Learning(NeurIPS'19)

• 파라미터를 sharing하며 새로운 task에 해당하는 optimal path를 찾는 random path selection 모델(이 과정에서 파라미터 share를 encourage 한다). CL에서의 과제인 stability와 plasticity의 trade-off를 해결하기 위함이다. 
  • 이는 (1) knowledge distillation 방법과 (2) path selection 과정에서의 retrospection, 그리고 (3) model plasticity (과거의 task를 얼마나 기억할 것인가)에 대한 dynamical controller와 dynamic path selection approach 까지 지금까지의 CL 방법들을 모두 조합한 알고리즘이다. 
  • 위 기존의 3가지 CL 방법이 각자 다른 단점을 가짐을 지적. 
• RPS-Net 아키텍처는 learnable sub-network인 $M_m^l$ 모듈(resnet block과 비슷)로 구성된다. 이러한 모듈이 $M$개 주어지고, $L$개의 layer로 구성될 때, 우리는 task 별 path를 다음과 같이 정의한다. 

 

• 따라서 이 path에서 $i$를 random하게 selection하여 $P_k$를 다음과 같이 계산한다. 그리고 path는 train에 사용하는 $P_k^{tr}$과 interence에 사용하는 $P_k^{ts}$로 나뉜다. 

 

• Path selection 과정은 $J$ task마다 적용하고, best path는 N개의 sub-model 중에 선택되며 이는 J task 동안 공유된다. (어느 point에서도 최대 1개의 모듈만 사용하여 효율성을 높임).
  • task K가 주어질 때 N개의 random path로 initialized 되고, 각 path는 previous inference path $P_{k-1}^ts$와 다른 모듈만 현재 task의 training path $P_k^{tr}$로 사용된다. 
  • N개의 path 중 optimal한 $P_k$가 선택되고, 이는 현재 test path를 얻기위해 이전 t-1 task의 test path $P_{k-1}^{ts}$와 결합된다. 

 

• Hybrid method이기 때문에 loss function은 regular cross-entropy loss와 distillation loss를 결합해 사용한다. 이 때, 두 loss를 결합할 때는 trade-off를 해결하기 위해 controller가 사용된다. 이는 network의 plasticity를 조절하기 위해 사용된다. 

---

2. FRCL

Functional Regularisation for continual learning with Gaussian Process (ICLR'20)

• 위에서 언급한 것처럼 기존 CL 방법들의 brittleness 문제와 heuristics 문제를 해결하기 위해 두 방법을 조합해서 사용한다. 이는 approximate bayesian inference 방법에 기반하고 있다.
  • Regularization 측면 : brittleness 문제를 막기 위해 network의 파라미터에 집중하기 보다 function space에 집중한다. (=파라미터를 constrain 하는게 아니라 neural network의 prediction에 집중함) 
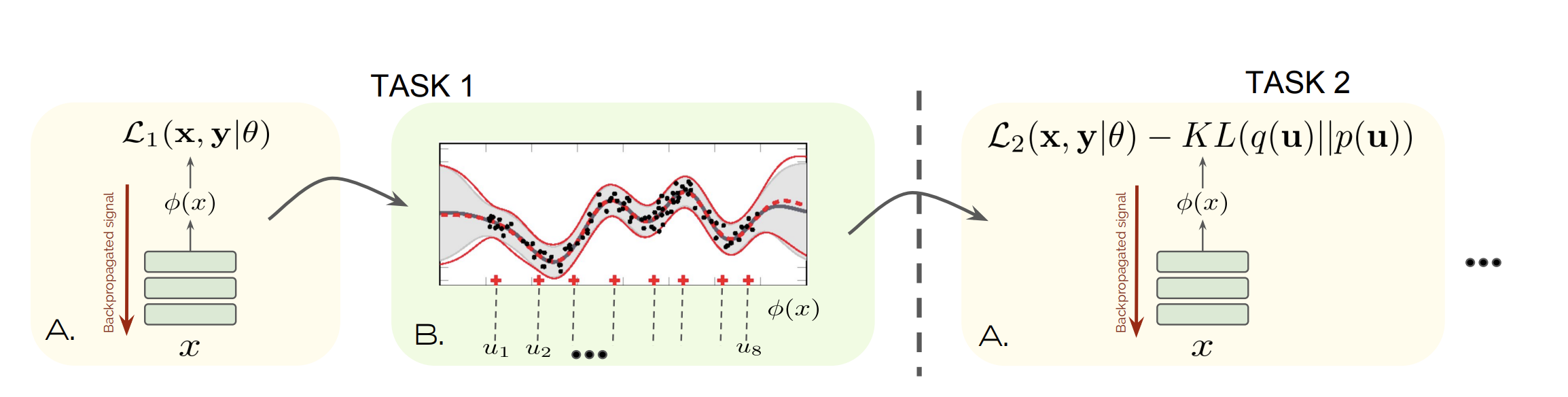
  • Rehearsal 측면 : approximate posterior belief를 memorize한다. 이를 위해 Gaussian processes(GPs)를 이용하며, GP mathods의 inducing point sparse(posterior distributions를 적은 수의 inducing point 들을 이용해 summarise 한다)를 이용한다. 이러한 inducing point들은 buffer 역할을 한다. 
  • 그리고 위에서 저장된 inducing point 들은 KL regularisation terms를 통해 future task를 regularise하는 데에 쓰인다. 

Task 1과 task 2를 학습하는 과정. u1.. u8까지는 inducing point들에 해당하고, 이렇게 저장된 inducing point 들은 KL divergence term으로 function을 regularise 하는 데에 쓰인다.

 

 

---

3. MC-SGD 

Linear Mode Connectivity in Multitask and Continual learning (ICLR'21)

• Multi-task learning과 Continual learning의 connectivity(=linear manifold가 존재함)를 최초로 밝힌 논문. 두 framework의 training regime를 생각해보면, 같은 starting point를 공유한다. (기존의 연구들로 미루어 봤을 때 initialization point는 두 solution의 connectivity에 큰 impact를 갖는다. 만약 initialize가 random하게 이루어진다면, connectivity를 찾기 어려울 것이라고 봄) 

두 task의 connectivity

• 하지만 위 MTL과 CL의 relation은 단순히 metric으로 정의하기에는 어려움이 있다. (e.g. Euclidean distance, Central Kernel Alignment(CKA)) 아래 그림에서 미루어 보듯 두 지표는 catastrophic forgetting을 잘 설명하지 못한다. 예를 들어 Euclidean distance는 CL task1 solution이 MTL task 5 solution보다 CL task 5 solution에 더 가깝다고 판단하기 때문이다. 

 

• 일단 MTL과 CL은 same initialization weight를 공유하므로 ($\hat(w)_1$, $w_1^*$), 두 task 사이 같은 linear connectivity가 적용되는지 확인하는게 목표였다. 하지만 아래로 미루어볼 때, MTL task 2 의 minima ($w_2^*$)는 CL의 task 1, task 2 minima($\hat(w)_1$, $\hat(w)_2$)와 connect 되어 있음을 알 수 있다. 
  • 따라서 MTL과 CL minima 사이에는 linear connectivity가 존재한다. 
  • 그렇다면 두 task 사이 linear path가 존재한다는 것이 무엇을 의미할까? TBD (작성자가 이해를 아직 완벽히 못함) 

같은 평면상에 위치한다.

 

• 위에서 밝혀낸 connectivity를 통해 replay와 regularization method를 합친 hybrid method인 MC-SGD를 제안한다. 이는 continual minima를 모든 previous minima의 low-loss valley에 위치하도록 constrain하는 것이다. 일단 $\hat(w_1)$과 $\hat(w_2)$의 linear connetivity를 enforce하는 loss는 다음과 같다. 

• 위 식을 decompose 하면 아래와 같이 나오는데, 이러한 mode connectivity loss는 regularization loss의 format을 가진다. 따라서 공통된 weight ($\bar(w)$)는 task 1과 task2의 loss를 동시에 minimize 하도록 강제된다. (공통된 CL minima의 low-loss path를 가지도록) 

 

• 또한 여기에 replay buffer를 사용해 이를 랜덤하게 구성하여 효율성을 높인다.