[선형대수] - (2) Solving Linear Equations

이 포스팅에서는 지난 포스팅에 이어 linear equation 관련된 이야기를 해보겠다. 선형대수에 관한 기초가 궁금하신 분은 이 전 게시물을 참고해주시면 된다! 참고로, 본 챕터에서 Elimination 연산에 관한 내용은 제외할 예정이다. 

2023.04.27 - [Linear Algebra] - [선형대수] - (1) Introduction to the vector

[선형대수] - (1) Introduction to the vector

 

# Row/Column picture

• 우리가 예전부터 알고있던 equations(방정식) format을 선형대수에서는 row picture과 column picture로 구분해서 보통 나타내곤 한다. Row picture은 우리에게 익숙하고, column picture이 선형대수에서 지향하는 바라고 이해하면 될 것 같다. 아래를 보면 이해가 쉽다. 

 

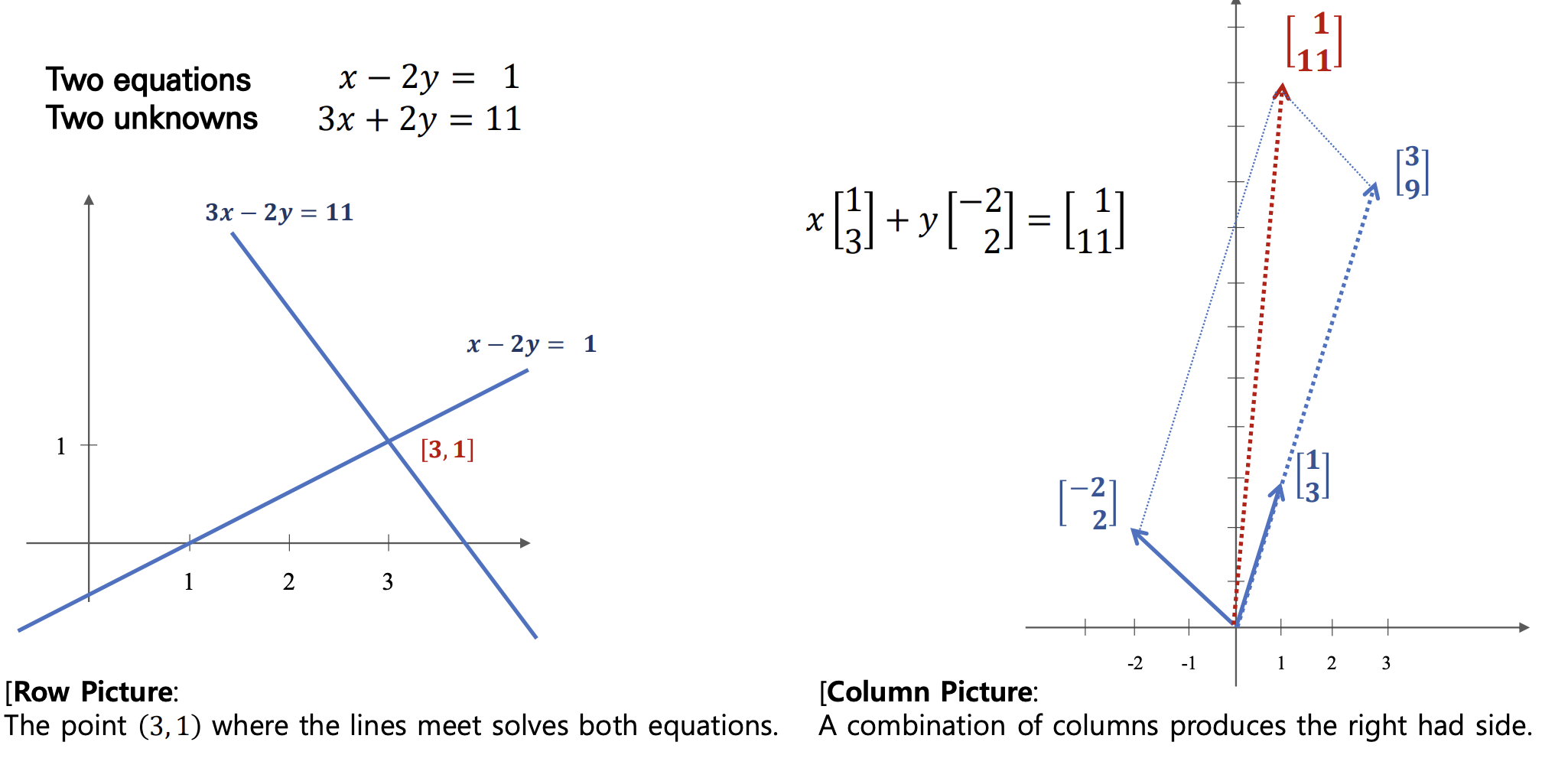
• 따라서 여기서 Equation의 해는 row picture의 경우 교점이 되고, column picture의 경우 두 column vector의 linear combination의 scalar가 된다.  아래와 같이 수식적으로 나타나진다. 
  • Row multiplication : dot product 
  • Column multiplication : column vector combination 

 

# Inverse matrix 

• 어떤 square matrix는 역행렬을 가질 수 있는데, 이 때 $A$의 역행렬을 $A^{-1}$이라고 부른다. 
• 역행렬에는 몇가지 성질이 존재하는데, 이를 정리하면 다음과 같다. 
  • 역행렬이 존재하면 $A$ matrix의 pivot은 n개이며 column 들은 모두 independent 하다. 
  • 역행렬은 unique 하다. 
  • 따라서 $Ax=b$ 방정식의 해도 unique하다. 직관적으로 $x=A^-1b$가 된다. 
  • $(AB)^{-1} = B^{-1} A^{-1}$ 
• 특히 2x2 matrix에서 역행렬은 아래와 같이 구한다. 3x3 이상은 elimination 과정으로 구해줘야 한다. 

역행렬 구하기

 

# Factorization : $A=LU$

• Elimination 과정을 통해 추출되는 pivot과 matrix $E$로 어떤 matrix를 $L$ (Lower triangle matrix), $U$ (Upper triangle matrix)로 분해할 수 있다. 

 

# Transpose 

• 행렬의 row와 column을 뒤집을 수 있는데, 이 때 $A$ 행렬의 transpose를 $A^T$라고 한다. 
• Transpose에는 아래와 같은 성질이 성립한다. 

 

# Symmetric matrices

• Diagonal 원소들을 중심으로 서로 대칭인 행렬을 symmetric matrix라고 부른다. 
• Symmetric matrix 들은 아래와 같은 성질을 가진다. 
  • Transpose 해도 같다. 즉, $S = S^T$ 
  • Inverse matrix도 symmetric matrix 이다. 
  • 앞에서 설명한 Factorization 과정을 $A=LDU$가 아니라 $S=LDL^T$로 나타낼 수 있다. 

 

# Permutation matrix 

• 어떤 matrix의 row 순서를 바꾸고 싶을 때, 앞에 Identity matrix의 해당 row를 바꾸어 곱해주는 형식으로 사용한다. 

• Permutation matrix는 다음과 같은 성질을 가진다. 
  • 역행렬인 $P^{-1}$ 또한 permutation matrix 이다. 
  • $P^{-1} = P^T$ 가 항상 성립한다. 
    • $PP^T = I$가 성립한다는 것이며, 이러한 matrix를 orthogonal matrix라고 부른다.