이 글은 고려대학교 통계학과 박유성 교수님의 '딥러닝을 위한 통계적 모델링' 강의를 바탕으로 재구성되었습니다.
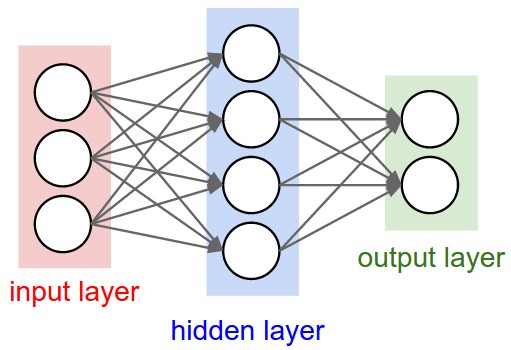
딥러닝과 통계적 모형의 구조는 매우 유사하지만, 다른점은 은닉층의 존재 여부이다.
따라서 은닉층의 설계에 따라 딥러닝 모형이 결정된다고 봐도 무방하다.
딥러닝은 특성변수들의 선형 결합을 비선형 변환해 목적변수를 확률적으로 맞추는 전형적인 통계적 모형이다. 이러한 과정을 통해 특성변수(x)를 변형시키고, 이러한 작업은 목적변수(y)를 더 잘 예측하게 한다.
다만 여기에 '은닉층(Hidden Layer)'의 개념이 포함된다는 것!
그래서 이 포스팅에서는 통계적 모형과 전반적인 딥러닝 구조의 유사성과 차이점에 대해 비교 대조해보고자 한다. 딥러닝을 공부해본 이래로 통계적인 해석을 한 글은 찾아보기 어려웠는데, 딥러닝을 통계적인 시각으로 바라볼 수 있다는 점이 놀랍다. (교수님 짱)
1. 통계적 모형 (Regression)
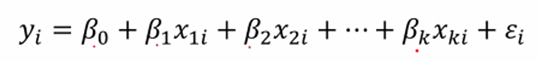
위 수식은 단순한 다중 선형회귀모형을 나타낸다. 회귀모형은 최소한의 모수로 구현된 모형으로 데이터의 특성을 파악한다.

이때 회귀선으로 적합된 적합값(Fitted Value)와 기존의 관측값의 오차를 계산하면 잔차(Residual)가 된다.
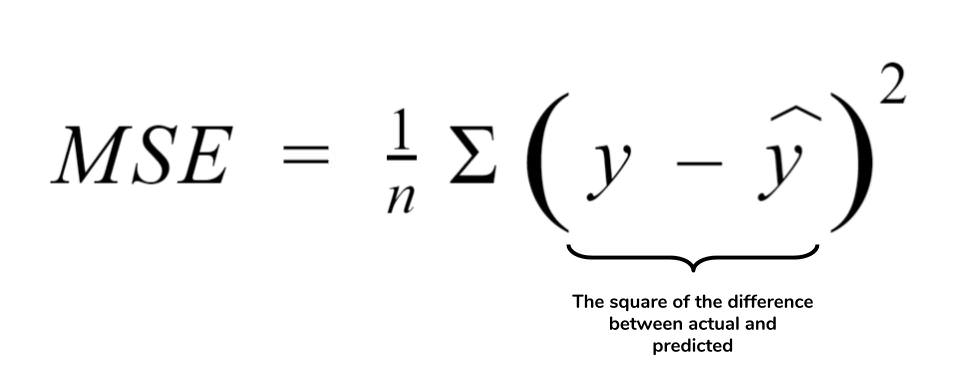
그리고 이러한 잔차 제곱합을 Minimize 하는 회귀 계수를 찾는 것이 통계적 모형(회귀모형)의 목적이라고 할 수 있다.
이 잔차는 회귀식에서 ε (오차항)을 추정하는 역할을 한다.
하지만, 이러한 잔차(residual)을 모두 0으로 만드는 것(최소로 만드는 것)이 정말 이상적인 상황일까?
아닐 수도 있다. 시각을 바꿔서 생각해보면 오차를 추정하는 잔차를 모두 0으로 만들게 되면 ε의 성격(분포)를 잘 담지 못한다. 즉, 오차항을 잔차가 잘못 추정할 수 있다는 것이다. 따라서 잔차는 원래 ε가 가지고 있는 확률 분포와 특성을 유지하려고 해야한다. 기계학습에서는 이러한 비슷한 현상을 '과적합'이라고 부르는 것이다.
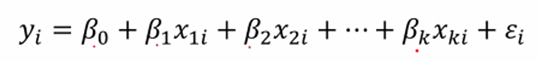
또한 이러한 모형에서 각 데이터들은 모수 β를 설명하는데 동일한 contribution을 해야한다. 이는 데이터들이 iid (즉, 독립이다) 라는 말과 일치하는 것이다. 이러한 상황에서 데이터는 uncertainty가 존재하게 된다.
만약, 데이터가 10 10 10 10 이라면 이는 strongly correlate되어있는 것이다. 즉, dependent 되어있다는 것이다. 이러한 상황에서는 모수 추론이 어렵다. 따라서 independent한 정보를 주어야만 모수 추론이 가능해진다.
2. 딥러닝의 구조
그렇다면 이러한 통계적 모형의 관점으로 딥러닝 구조를 바라본다면 어떨까?
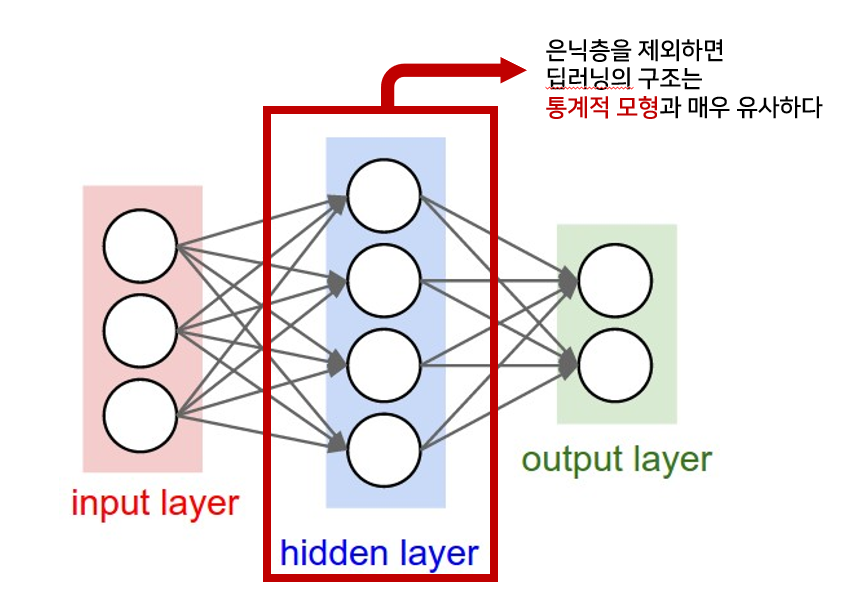
딥러닝은 입력충의 출력이 첫번째 은닉층의 입력으로 들어가고, 마지막 은닉층의 출력이 출력층의 입력으로 들어가는 형태이다. 따라서 앞 모수를 변동시키면 뒤 모수까지 모두 변동시켜 업데이트 해줘야 하는 문제가 발생하는 것이다(Back Propagation) 또한 이러한 과정에서 우리가 잘 알고있는 Gradient Vanishing 문제가 발생한다.
여기서 은닉층을 제외하면 input과 output이 존재하는 통계적 모형과 매우 유사해진다. 이러한 은닉층에서는 Activation Function을 통한 비선형변환을 통해 매개변수 X를 계속 업데이트하여 y를 가장 잘 설명하는 매개변수를 도출한다.
만약 k개의 특성변수가 입력층으르 들어가는 딥러닝 구조의 상황을 가정해보자.

전반적인 수식으로 표현하면 다음과 같다. 첫 줄은 통계적 모형의 linear combination과 매우 유사하지만 m개의 linear combination이 존재한다는 점은 다르다. (통계학에서는 하나만 존재한다) 따라서 통계적 모형에서 모수는 k개가 되지만, 딥러닝에서 모수의 개수는 m*k개가 된다.
따라서 m개의 값이 Activation Function을 통과해 비선형으로 변형되고, k개의 x값에서 m개의 y값이 도출되게 된다 (linear combination이 m개이기 때문이다)

그림으로 나타내면 다음과 같다. k개의 input에서 m개의 output이 출력되어 다음 은닉층으로 들어가는 구조이고, 모수의 개수는 k*m개가 된다. w가 k개씩 m개 존재하기 때문이다. 여기서 w는 선형결합에 사용되는 가중치로, 통계적 모형의 β와 비슷한 역할을 한다.
역시 이 모수들은 표본에 의존하지 않는다. 각 표본은 특성변수의 선형결합에 동일한 contribution을 낸다는 뜻으로 통계적모형도 이와 같다. 각 표본은 통계적으로 같은 분포에서 나온 정보이며 서로간에 독립이라는 의미를 갖는다.
cf) 표본의 독립성(Uncertainty)
동일한 특성변수에 서로 다른 목적변수가 관측되고, 동일한 목적변수에 서로 다른 특성변수도 관측되는 현상. 이는 딥러닝모형의 일반화에 매우 중요한 역할을 한다.
다음 은닉층으로 들어간다는 의미는 비선형 변환을 통해 특성변수를 계속 만들어낸다는 의미가 된다. 이걸 계속 반복하면, 모수(w)의 개수는 계속 기하급수적으로 증가한다. 이러한 과정으로 x를 선형-비선형으로 바꾸는것을 반복함으로써 y를 가장 잘 설명하는 최적의 매개변수를 만들어내는 것이다.
그래서 딥러닝 구조는 기하급수적인 모수를 가지기때문에 Overfitting을 어떻게 처리할 것인가가 정말 중요한 문제이다.
또한 출력층에서 손실함수와 loss를 줄이는 방향으로 모수(가중치)를 업데이트 하는 모수 최적화를 거치기 때문에, loss를 계산하는 과정 역시 통계적 모형과 유사하다.
딥러닝과 기계학습의 근간은 역시 통계학이라는 점을 유의해야할 것 같다.
'Computer Vision💖 > Basic' 카테고리의 다른 글
| [CV] Adversarial Learning(적대적 학습)이란? + 응용 (0) | 2022.04.24 |
|---|---|
| [CV] Self-supervised learning(자기주도학습)과 Contrastive learning - 스스로 학습하는 알고리즘 (4) | 2021.07.02 |
| [CV] AlexNet(2012) 논문을 code로 구현 해보자 (Keras, PyTorch) (0) | 2021.06.25 |
| [CV] AlexNet(2012)의 구조와 논문 리뷰 (0) | 2021.06.23 |
| [CV] ResNet - Residual Connection(잔차연결) (0) | 2021.05.04 |
![[STAT & DL] 딥러닝의 전반적 구조에 대한 통계적 해석](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FOUnOO%2FbtqZjv1qtzs%2FAAAAAAAAAAAAAAAAAAAAABQSiVvt_G4devLujI1_IK6EOrVXQf_28YFKQJgHn2Vn%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3De13wyLnd3i61UTdtyI%252FVvLatyVg%253D)